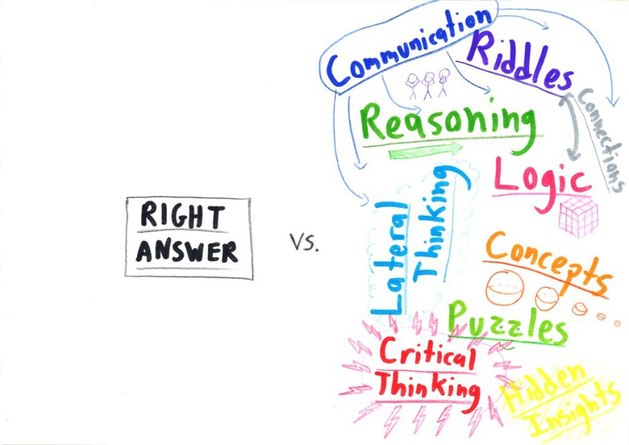
Here it was, out in the open: the subtext of practically every class I’ve ever taught. I’ve grown accustomed to yanking my side of the rope in an unspoken tug-of-war. The teacher emphasizes conceptual understanding. The students conspire to find shortcuts around it. So it always goes.
This is something my department has been talking a lot about recently and trying to make sense of how the network our school is in (Expeditionary Learning) wants us to build in comprehension in our lessons. It usually involves making things a lot slower than the traditional class might look like, but the students end up with such a deeper level of knowledge it becomes worth it.
While reading Ben Orlin's post about this "church" I was reminded of an article I read in early January about "why the phrase 'math facts' is so dangerous." In it the author asserts (much like Orlin) that to memorize information is not to truly understand it and therefore it will not work in application to novel situations. The simple idea of memorizing multiplication tables is a good example. While knowing those can be useful at times, when dealing with larger numbers it breaks down, whereas if you understand place value and it's effect on operations you will be able to scale up your knowledge.
I fully support students gaining a deeper understanding and how that I can bring my own up to that level. Then maybe they'll understand the battle should really be won because "the right answer" is on one side by itself.



 RSS Feed
RSS Feed
