The idea is simple: there are differently-sized infinities.
But the explanation can get complex:
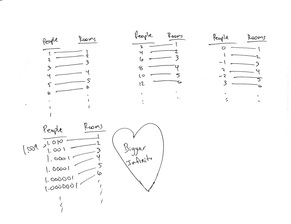
Then say you have guests with number badges to make assigning rooms easier. With Group A, the number badges are the set of Natural Numbers (counting numbers that begin with 1). So, according to the image above, 1->1, 2->2, 3->3, etc. Each person is given a room. Great - that seemingly makes sense.
But now say you have Group B, whose number badges are the set of Even Numbers (only positive integers divisible by 2). Now you have Person #2 going to Room #1. That's okay, right? And Person #4 goes to Room #2. That's also okay. This continues with 6->3, 8->4, etc. And it goes to infinity. The kicker here is that it is the same infinity as Group A. That usually confuses people but the idea is sound. All members of Group B get a room at the hotel, and it is the exact same rooms as Group A.
Now you have Group C whose number badges are all the Integers (positive, negative, and zero). There is no "beginning" of this list like with Group A and B because they go on forever in both positive and negative directions. So the best way to assign them rooms is to start with 0, then alternate 1, -1, then 2, -2, and so on. As it turns out, this mapping is the same size as Groups A and B. This gets really confusing to many because they say "but there are SO many more numbers with the negatives involved!" Sorry, folks, but since each person in Group C can get a room, and they are the same rooms as the other groups, then technically, Groups A, B, and C are all the same-sized infinity.
There are a lot more examples that could be done to show the same size, so now let's see a differently sized one. Take the real numbers. Group D has people with numbers like 1.01, 1.001, 1.001, 1.0001, and all numbers in between. So if you try to assign room numbers using the system in place, we could take 1.01->1, 1.001->2, 1.0001->3, etc. So, technically, if we continue the pattern of adding a 0 in between the ones, we would use up all the rooms. The problem comes in when you realize there are other numbers in this sequence. Case in point : 1.009. Where does that person go? Since all the rooms are used up already from the pattern identified, then this set of numbers must be a bigger infinity.
If you want to get more in depth on the subject, there is a short article in Scientific American from 2007 that describes this phenomenon with mathematical language.


 RSS Feed
RSS Feed
